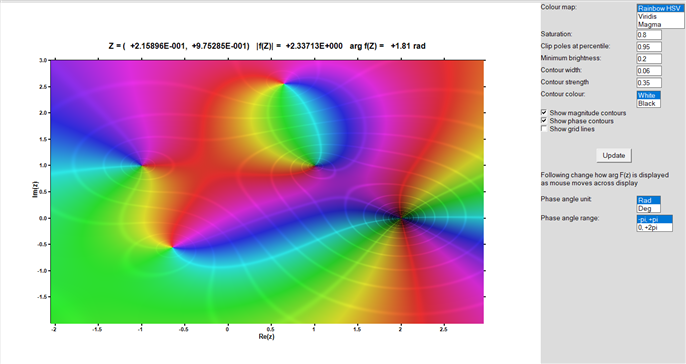
The domain_plot_mod module provides an interactive ClearWin+–based visualization tool for complex-valued functions over a two-dimensional real domain. Given strictly monotonic real coordinate arrays x and y (not necessarily uniform) and a sampled complex field z(x,y), the subroutine DOMAIN_PLOT(x,y,z) renders a phase–magnitude domain plot in which amplitude is mapped to perceptual brightness, and phase is overlaid through hue (for HSV) or optional contour structures. The code performs preprocessing including safe logarithmic scaling of magnitudes, adaptive percentile-based clipping to control extreme poles, and bilinear interpolation of amplitude and phase using unit-circle projections to avoid angular discontinuities. Rendering is handled pixel-by-pixel via a plotting callback, supporting multiple colour maps (Rainbow/HSV, Viridis, and Magma), adjustable saturation and brightness floors, optional magnitude and phase contours blended toward white or black, and interactive mouse readout of complex values with selectable angle units and ranges. The design emphasizes perceptual clarity and interactive exploration of complex function behaviour while remaining efficient and compatible with native ClearWin+ graphics primitives.
module domain_plot_mod
use clrwin
implicit none
private
public domain_plot
real*8, allocatable :: xc(:), yc(:), amp(:,:), phase(:,:), &
zabslog1psorted(:), ccos(:,:), csin(:,:)
real*8, parameter :: pi = 4.d0*atan(1.d0), twopi = 2.d0*pi
real*8, parameter :: halfpi = 0.5d0*pi, rec2pi = 1.d0/(2.d0*pi)
real*8, parameter :: rad2deg = 180.d0/pi
real*8, parameter :: log2 = log(2.d0), reclog2 = 1.d0/log2
real*8 :: xmin, xmax, ymin, ymax, zabsmin, zabsmax
integer :: screen_width, screen_depth, graphics_width, graphics_depth
integer :: mleft, mtop, mright, mbottom, fleft, ftop, fright, fbottom
integer :: frame_center_x, frame_width
integer :: show_mag_contours, show_phase_contours,show_grid_lines
real*8 :: perc, sat, v_min, width, strength
logical :: first_plot_adjust
integer :: menu_on = 1
character(len=5), parameter :: contour_colour(2) = ['White','Black']
integer :: contour_colour_selected = 1
character(len=5), parameter :: phase_angle(2) = ['Rad ','Deg ']
integer :: phase_angle_selected = 1
character(len=8), parameter ::phase_angle_range(2) = ['-pi, +pi','0, +2pi ']
integer :: phase_angle_range_selected = 1
character(len=11), parameter :: colour_map(4) = ['Rainbow HSV','Viridis ',&
'Magma ','Turbo ']
integer :: colour_map_selected = 1
! --------------------------------------------------------------------
! Viridis colormap
! Source: Matplotlib (Stefan van der Walt, Nathaniel Smith, Eric Firing)
! Licence: CC0 1.0 Universal (public domain, no restrictions)
! --------------------------------------------------------------------
real*8, parameter :: viridis18(18,3) = reshape([ &
! R column (18)
0.267004,0.281924,0.280255,0.263663,0.237441,0.208623,&
0.182256,0.159194,0.137770,0.121148,0.128087,0.180653,&
0.274149,0.395174,0.535621,0.688944,0.845561,0.993248,&
! G column (18)
0.004874,0.089666,0.165693,0.237631,0.305202,0.367752,&
0.426184,0.482237,0.537492,0.592739,0.647749,0.701402,&
0.751988,0.797475,0.835785,0.865448,0.887322,0.906157,&
! B column (18)
0.329415,0.412415,0.476498,0.518762,0.541921,0.552675,&
0.557120,0.558073,0.554906,0.544641,0.523491,0.488189,&
0.436601,0.367757,0.281908,0.182725,0.099702,0.143936],[18,3])
! --------------------------------------------------------------------
! Magma colormap
! Source: Matplotlib (Stefan van der Walt, Nathaniel Smith, Eric Firing)
! Licence: CC0 1.0 Universal (public domain, no restrictions)
! --------------------------------------------------------------------
real*8, parameter :: magma18(18,3) = reshape([ &
! R column (18)
0.001462,0.035520,0.102815,0.191460,0.291366,0.384299,&
0.475780,0.569172,0.664915,0.761077,0.852126,0.925937,&
0.969680,0.989363,0.996580,0.996727,0.992440,0.987053,&
! G column (18)
0.000466,0.028397,0.063010,0.064818,0.064553,0.097855,&
0.134577,0.167454,0.198075,0.231214,0.276106,0.346844,&
0.446936,0.557873,0.668256,0.776795,0.884330,0.991438,&
! B column (18)
0.013866,0.125209,0.257854,0.396152,0.475462,0.501002,&
0.507921,0.504105,0.488836,0.460162,0.418573,0.374959,&
0.360311,0.391671,0.456192,0.541039,0.640099,0.749504],[18,3])
! --------------------------------------------------------------------
! Turbo colourmap (Google, 2019)
! Source: Anton Mikhailov, Google AI Blog
! Licence: Apache 2.0 (permissive, attribution recommended)
! 18-sample turbo, arranged as R-block, then G-block, then B-block
! --------------------------------------------------------------------
real*8, parameter :: turbo18(18,3) = reshape([ &
! R column (18)
0.189950,0.248300,0.275090,0.268780,0.186250,0.100260, &
0.135260,0.320060,0.546580,0.715770,0.858680,0.960490, &
0.996540,0.975450,0.910240,0.807990,0.664490,0.479600, &
! G column (18)
0.071760,0.241430,0.400720,0.549950,0.697750,0.829550, &
0.921970,0.979740,0.999070,0.968750,0.886550,0.771810, &
0.631930,0.457400,0.295990,0.177530,0.084360,0.015830, &
! B column (18)
0.232170,0.612860,0.866920,0.993030,0.954980,0.813890, &
0.665560,0.476540,0.295810,0.208150,0.212300,0.228110, &
0.187380,0.113050,0.048140,0.016600,0.004240,0.010550 ], [18,3])
contains
subroutine domain_plot(x,y,z)
real*8, intent(in) :: x(:)
real*8, intent(in) :: y(:)
complex*16, intent(in) :: z(:,:)
integer :: i, j, k, nx, ny, iw
logical :: ismonotonicinc
nx = size(x) ; ny = size(y)
if (size(z,dim=1) .ne. nx .or. size(z,dim=2) .ne. ny) &
STOP 'Non-conformant arrays in call to DOMAIN_PLOT'
! Check that x and y are strictly monotonic increasing
ismonotonicinc = .true.
do i = 1, nx -1
if (x(i+1) <= x(i)) then
ismonotonicinc = .false.
exit
end if
end do
if (ismonotonicinc) then
do j = 1, ny-1
if (y(j+1) <= y(j)) then
ismonotonicinc = .false.
exit
end if
end do
end if
if (.not. ismonotonicinc) then
print*, 'DOMAIN_PLOT: x and/or y are not strictly monotonic increasing'
return
end if
! Allocate storage arrays
if (allocated(xc)) deallocate(xc)
if (allocated(yc)) deallocate(yc)
if (allocated(amp)) deallocate(amp)
if (allocated(phase)) deallocate(phase)
if (allocated(zabslog1psorted)) deallocate(zabslog1psorted)
if (allocated(ccos)) deallocate(ccos)
if (allocated(csin)) deallocate(csin)
allocate (xc(nx),yc(ny),amp(nx,ny),phase(nx,ny),zabslog1psorted(nx*ny),ccos(nx,ny),csin(nx,ny))
xmin = x(1) ; xmax = x(nx) ; ymin = y(1) ; ymax = y(ny)
! Copy arguments x and y to global module arrays xc and yc to make
! them accessible later
xc = x ; yc = y
! Do some preprocessing before the pl callback
zabsmin = huge(1.d0)
zabsmax = 0.d0
k = 0
do j = 1, ny
do i = 1, nx
amp(i,j) = abs(z(i,j))
zabsmin = min( zabsmin, amp(i,j) )
zabsmax = max( zabsmax, amp(i,j) )
if (amp(i,j) > 1.0d-300) then
phase(i,j) = atan2(aimag(z(i,j)), real(z(i,j)))
else
! Avoid "starbust"
phase(i,j) = phase(max(1,i-1),max(1,j-1))
end if
! Projections onto the unit circle
ccos(i,j) = cos(phase(i,j))
csin(i,j) = sin(phase(i,j))
! Flatten log(1+|Z|) into vector - sorted later
k = k + 1
zabslog1psorted(k) = safe_log1p(amp(i,j))
end do
end do
! Sort zabslog1psorted once, so don't need to do again if
! percentile cut off changed
call quicksort(zabslog1psorted)
if (zabsmax > zabsmin) then
! Prevent first render being performed before the window appears
first_plot_adjust = .true.
screen_width = clearwin_info@('SCREEN_WIDTH')
screen_depth = clearwin_info@('SCREEN_DEPTH')
graphics_width = int(0.6d0*dble(screen_width))
graphics_depth = int(0.7d0*dble(screen_depth))
call calc_pl_margins(graphics_width, graphics_depth, mleft, mtop, mright, mbottom)
! Default pl margins are relatively large for large regions, reduce by 2/3
mleft = 2*mleft/3
mtop = 2*mtop/3
mright = 2*mright/3
mbottom = 2*mbottom/3
ftop = mtop
fbottom = graphics_depth - mbottom
fleft = mleft
fright = graphics_width - mright
frame_width = graphics_width - mleft - mright
frame_center_x = mleft + frame_width/2
! Set default plotting parameters
show_mag_contours = 1
show_phase_contours = 1
show_grid_lines = 0
sat = 0.8d0
v_min = 0.2d0
width = 0.06d0
strength = 0.35d0
! Choose good percentile value for pole clipping using adaptpercentile
perc = adaptpercentile(zabslog1psorted)
iw = winio@('%ww[no_sysmenu]&')
iw = winio@('%mn[~Exit]&',menu_on,'exit')
iw = winio@('%mn[~Help]&',menu_on,help_cb)
iw = winio@('%fn[Arial]%ts%bf%bg&',1.2d0,rgb@(220,220,220))
call winop@('%pl[native, n_graphs=1,x_array,frame,link=user,external_ticks]')
call winop@('%pl[axes_pen=2,frame_pen=2,xaxis="Re(z)",yaxis="Im(z)"]')
call winop@('%pl[full_mouse_input,gridlines]')
call winop_flt@('%pl[x_min]',xmin)
call winop_flt@('%pl[x_max]',xmax)
call winop_flt@('%pl[y_min]',ymin)
call winop_flt@('%pl[y_max]',ymax)
call set_pl_margins(mleft, mtop, mright, mbottom)
iw = winio@('%2.1ob[invisible]&')
iw = winio@('%^pl&',graphics_width,graphics_depth,2,[0.d0,1.d0],[0.d0,1.d0],pl_cb)
iw = winio@('%cb&')
iw = winio@('%sf&')
iw = winio@('%fl&',0.d0,1.d0)
iw = winio@('Colour map:%ta%ta%`bg[white]%ls%ff&', &
colour_map, 4, colour_map_selected)
iw = winio@('Saturation:%ta%ta%`bg[white]%6rf%nl&',sat)
iw = winio@('Clip poles at percentile:%ta%`bg[white]%6rf%nl&',perc)
iw = winio@('Minimum brightness:%ta%ta%`bg[white]%6rf%nl&',v_min)
iw = winio@('Contour width:%ta%ta%`bg[white]%6rf%nl&',width)
iw = winio@('Contour strength%ta%ta%`bg[white]%6rf%nl&',strength)
iw = winio@('Contour colour:%ta%ta%`bg[white]%ls%ff&',contour_colour,2,contour_colour_selected)
iw = winio@('%`fl&')
iw = winio@('%`rb[Show magnitude contours]%nl&',show_mag_contours)
iw = winio@('%`rb[Show phase contours]%nl&',show_phase_contours)
iw = winio@('%`rb[Show grid lines]%nl&',show_grid_lines)
iw = winio@('%2nl%cn%~^bn[Update]%2nl&',menu_on,update_cb)
iw = winio@('Following change how arg F(z) is displayed%nlas mouse moves across display%2nl&')
iw = winio@('Phase angle unit:%ta%ta%`bg[white]%ls%ff&',phase_angle,2,phase_angle_selected)
iw = winio@('Phase angle range:%ta%ta%`bg[white]%ls%ff&',phase_angle_range,2,phase_angle_range_selected)
iw = winio@('%cb&')
iw = winio@('%sc&',sc_cb)
iw = winio@('')
else
print*, 'Domain_plot: Input is level plane.'
end if
end subroutine domain_plot
!----------------------------------------------------------------
integer function sc_cb()
!----------------------------------------------------------------
first_plot_adjust = .false.
sc_cb = update_cb()
end function sc_cb
!----------------------------------------------------------------
integer function update_cb()
!----------------------------------------------------------------
call set_cursor_waiting@(1)
call simpleplot_redraw@()
call set_cursor_waiting@(0)
update_cb = 2
end function update_cb
!----------------------------------------------------------------
recursive integer function pl_cb()
!----------------------------------------------------------------
integer :: i, j, k, icol
integer :: mouse_x, mouse_y
real*8 :: x, y, r, h
real*8 :: red, green, blue, t, f, d, line
real*8 :: target_phase, fphase
real*8 :: v, scale_factor
real*8 :: mag, angle, xperc, recw2, v_target
integer :: text_x, text_y, tw, th, idx, npoints
integer(2) :: i2, j2
integer :: val
real*8, parameter :: ref_mag = 1000.d0
real*8, parameter :: width_min = 1.0d-6
character(len=256) ::clearwin_string@, cb_reason
character(len=512) ::data_string
character(len=*), parameter :: fmt1 = '( &
& "Z = (",1X,SP,ES14.5E3,",",1X,SP,ES14.5E3,")",3X, &
& "|f(Z)| =",1X,SP,ES14.5E3,3X, &
& "arg f(Z) =",1X,SP,F7.2,1X,"rad")'
character(len=*), parameter :: fmt2 = '( &
& "Z = (",1X,SP,ES14.5E3,",",1X,SP,ES14.5E3,")",3X, &
& "|f(Z)| =",1X,SP,ES14.5E3,3X, &
& "arg f(Z) =",1X,SP,F7.1,1X,"deg")'
logical, save :: pl_cb_active = .false.
logical, save :: first = .true.
integer,save :: iwhite, iblack
if (pl_cb_active) then
pl_cb = 2
return
end if
if (first) then
iwhite = rgb@(255,255,255)
iblack = rgb@(0,0,0)
first = .false.
end if
pl_cb_active = .true.
menu_on = 0
cb_reason = clearwin_string@('CALLBACK_REASON')
if (cb_reason .eq. 'RESIZE') then
pl_cb_active = .false.
menu_on = 1
pl_cb=2
return
else if (cb_reason .eq. 'MOUSE_MOVE') then
mouse_x = clearwin_info@('GRAPHICS_MOUSE_X')
mouse_y = clearwin_info@('GRAPHICS_MOUSE_Y')
call draw_filled_rectangle@(0, int(0.9d0*dble(mtop)), graphics_width,0, iwhite)
if (mouse_x .ge. fleft .and. mouse_x .le. fright .and. &
mouse_y .ge. ftop .and. mouse_y .le. fbottom) then
k = get_plot_data@(mouse_x,mouse_y,x,y)
if (k == 0 .and. x >= xmin .and. x <= xmax .and. y >= ymin .and. y <= ymax) then
call z_rh_bilinear(x,y,mag,angle)
if (phase_angle_range_selected .eq. 2) then
if (angle < 0.d0) angle = angle + twopi
end if
if (phase_angle_selected .eq. 1) then
write(data_string,fmt1) x, y, mag, angle
else
write(data_string,fmt2) x, y, mag, angle*rad2deg
end if
call get_text_size@(trim(adjustl(data_string))//char(0), tw, th)
text_x = frame_center_x - tw/2
text_y = ftop - th - 20 ! small gap above frame
call draw_characters@(data_string, text_x, text_y, iblack)
end if
end if
pl_cb_active = .false.
menu_on = 1
pl_cb=2
return
else if (cb_reason .eq. 'PLOT_ADJUST') then
if (first_plot_adjust) then
pl_cb_active = .false.
pl_cb = 2
return
end if
npoints = size(zabslog1psorted)
idx = max(1, min(npoints, nint(perc * dble(npoints))))
xperc = zabslog1psorted(idx)
xperc = exp(xperc) - 1.d0
! Guard against zero percentile
scale_factor = 1.d0
if (xperc > 0.d0) scale_factor = ref_mag / xperc
recw2 = 1.d0/(width*width)
!set v_target for contour colours
if (contour_colour_selected .eq. 1) then
! White
v_target = 1.d0
else
! Black
v_target = 0.d0
end if
! Render the surface
do i = fleft, fright, 1
do j = fbottom, ftop, -1
k = get_plot_data@(i,j,x,y)
! Don't draw over grid lines if show_grid_lines = 1
if (show_grid_lines .eq. 1) then
i2 = i ; j2 = j
call get_rgb_value@(i2,j2,val)
if (val .ne. iwhite) cycle
end if
! Interpolate amplitude and phase
call z_rh_bilinear(x,y,r,h)
h = (h + pi) * rec2pi
h = h - floor(h)
r = r*scale_factor
! Base brightness from amplitude
v = 1.d0 - 1.d0/(1.d0 + safe_log1p(r))
!!v = safe_log1p(r) / safe_log1p(r + 1.d0)
v = max(v, v_min)
! Magnitude contours (white or black rings)
if (show_mag_contours == 1) then
if (r > 0.d0 .and. width > width_min) then
t = log(r)*reclog2
f = t - floor(t)
d = min(f, 1.d0 - f)
line = exp(-d*d*recw2)
! Blend towards selected contour colour
v = v + (v_target - v)*line*strength
end if
end if
! Phase contours (white or black lines)
if (show_phase_contours == 1 .and. width .gt. width_min) then
do k = 0, 3
target_phase = halfpi*dble(k)
fphase = abs(h*twopi - target_phase)
if (fphase > pi) fphase = twopi - fphase
line = exp(-fphase*fphase*recw2)
! Blend towards selected contour colour
v = v + (v_target - v)*line*strength
end do
end if
! Final clamp of brightness
v = min(1.d0, max(v_min, v))
! Convert HSV or V to RGB depending on selected colour map
select case(colour_map_selected)
case(1) ; call hsv_to_rgb(h, sat, v, red, green, blue)
case(2) ; call cmap_rgb(viridis18,v, red, green, blue)
case(3) ; call cmap_rgb(magma18,v, red, green, blue)
case(4) ; call cmap_rgb(turbo18,v, red, green, blue)
end select
icol = rgb@(int(255.d0*red), int(255.d0*green), int(255.d0*blue))
! Draw pixels using draw_filled_rectangle@
call draw_filled_rectangle@(i,j,i,j,icol)
end do
if (mod(i,2) == 0) call temporary_yield@()
end do
menu_on = 1
pl_cb_active = .false.
pl_cb = 2
return
end if
! Defensive, should never get here
menu_on = 1
pl_cb_active = .false.
pl_cb = 2
end function pl_cb
!----------------------------------------------------------------
subroutine z_rh_bilinear(xt, yt, r, h)
!----------------------------------------------------------------
real*8, intent(in) :: xt, yt
real*8, intent(out) :: r, h
integer, save:: i=1, j=1
real*8 :: x1, x2, y1, y2, tx, ty
real*8 :: c, s, rrr
! Uses global arrays yc, xc, amp, ccos, csin
! Locate cell
i = bin_search2(xc, xt, i) ; j = bin_search2(yc, yt, j)
x1 = xc(i) ; x2 = xc(i+1) ; y1 = yc(j) ; y2 = yc(j+1)
tx = (xt - x1) / (x2 - x1) ; ty = (yt - y1) / (y2 - y1)
! Bilinear interpolation of amplitude
r = (1.d0-tx)*(1.d0-ty)*amp(i, j ) + tx*(1.d0-ty)*amp(i+1,j ) + &
(1.d0-tx)*(ty )*amp(i, j+1) + tx*(ty )*amp(i+1,j+1)
! Bilinear interpolation on unit circle
c = (1.d0-tx)*(1.d0-ty)*ccos(i, j ) + tx*(1.d0-ty)*ccos(i+1,j ) + &
(1.d0-tx)*(ty )*ccos(i, j+1) + tx*(ty )*ccos(i+1,j+1)
s = (1.d0-tx)*(1.d0-ty)*csin(i, j ) + tx*(1.d0-ty)*csin(i+1,j ) + &
(1.d0-tx)*(ty )*csin(i, j+1) + tx*(ty )*csin(i+1,j+1)
! Normalise and recover phase
rrr = hypot(c,s)
h = 0.d0
if (rrr > 0.d0) h = atan2(s/rrr, c/rrr)
end subroutine z_rh_bilinear
!----------------------------------------------------------------
subroutine hsv_to_rgb(h, s, v, r, g, b)
!----------------------------------------------------------------
real*8, intent(in) :: h, s, v
real*8, intent(out) :: r, g, b
real*8 :: i, f, p, q, t
i = floor(6.d0*h) ; f = 6.d0*h - i
p = v*(1.d0 - s) ; q = v*(1.d0 - f*s)
t = v*(1.d0 - (1.d0-f)*s)
select case (mod(int(i),6))
case (0); r=v; g=t; b=p
case (1); r=q; g=v; b=p
case (2); r=p; g=v; b=t
case (3); r=p; g=q; b=v
case (4); r=t; g=p; b=v
case (5); r=v; g=p; b=q
end select
end subroutine hsv_to_rgb
!----------------------------------------------------------------
subroutine calc_pl_margins(width, height, left, top, right, bottom)
!----------------------------------------------------------------
integer, intent(in) :: width, height
integer, intent(out) :: left, top, right, bottom
integer :: m, hoffset, voffset
m = max( 28, int(0.1d0 * max(width, height)) )
bottom = m ; right = m
hoffset = m / 2 ; voffset = 0
left = m + hoffset ; top = m + voffset
end subroutine calc_pl_margins
!----------------------------------------------------------------
subroutine quicksort(a)
!----------------------------------------------------------------
! Textbook recursive quicksort
!----------------------------------------------------------------
real*8, intent(inout) :: a(:)
call qs(a, 1, size(a))
contains
recursive subroutine qs(a, left, right)
real*8, intent(inout) :: a(:)
integer, intent(in) :: left, right
integer :: i, j
real*8 :: pivot, tmp
if (left >= right) return
pivot = a((left+right)/2)
i = left ; j = right
do
do while (a(i) < pivot)
i = i + 1
end do
do while (a(j) > pivot)
j = j - 1
end do
if (i <= j) then
tmp = a(i) ; a(i) = a(j) ; a(j) = tmp
i = i + 1 ; j = j - 1
end if
if (i > j) exit
end do
call qs(a, left, j)
call qs(a, i, right)
end subroutine qs
end subroutine quicksort
!----------------------------------------------------------------
real*8 function safe_log1p(x)
!----------------------------------------------------------------
! Returns log(1+x) safely for x > -1
!----------------------------------------------------------------
real*8, intent(in) :: x
real*8 :: ax
real*8, parameter :: x_tiny = sqrt(epsilon(1.d0))
ax = abs(x)
if (x <= -1.d0) then
safe_log1p = -huge(1.d0)
else if (ax < x_tiny) then
safe_log1p = x*(1.d0 - x*(0.5d0 - x*(1.d0/3.d0)))
else if (x > huge(1.d0)/2.d0) then
safe_log1p = log(x)
else
safe_log1p = log(1.d0 + x)
end if
end function safe_log1p
real*8 function adaptpercentile(zlog)
!-------------------------------------------------------------------
! Compute an adaptive percentile for amplitude clipping
! Input: zlog(:) = log1p(abs(z)) sorted ascending
! Output: adaptive_percentile = suggested percentile [0,1]
!-----------------------------------------------------------------------
! Tail Ratio Interpretation Adaptive
! (q99-q50)/(q95-q50) percentile
!-----------------------------------------------------------------------
! < 0.5 Very light tail 0.99
! < 1.0 Light tail, mild outliers 0.97
! < 2.0 Moderate tail 0.95
! < 4.0 Heavy tail 0.92
! >= 4.0 Extreme tail (very large poles) 0.90
!-----------------------------------------------------------------------
real*8, intent(in) :: zlog(:)
integer :: n
real*8 :: q50, q95, q99, tail_ratio
real*8, parameter :: default_perc = 0.95d0
n = size(zlog)
if (n < 10) then
! Too few points, fallback
adaptpercentile = default_perc
return
end if
! Fetch percentile values
q50 = zlog(max(1, min(n, nint(0.50d0 * dble(n)))))
q95 = zlog(max(1, min(n, nint(0.95d0 * dble(n)))))
q99 = zlog(max(1, min(n, nint(0.99d0 * dble(n)))))
! Guard against degenerate cases
if (q95 <= q50) then
adaptpercentile = 0.95d0
return
end if
! Tail ratio: how far the extreme tail is from the bulk
tail_ratio = (q99 - q50) / (q95 - q50)
! Map tail_ratio to adaptive percentile
if (tail_ratio < 0.5d0) then
adaptpercentile = 0.99d0
else if (tail_ratio < 1.0d0) then
adaptpercentile = 0.97d0
else if (tail_ratio < 2.0d0) then
adaptpercentile = 0.95d0
else if (tail_ratio < 4.0d0) then
adaptpercentile = 0.92d0
else
adaptpercentile = 0.90d0
end if
end function adaptpercentile
!----------------------------------------------------------------
subroutine cmap_rgb(cmap,t, r, g, b)
!----------------------------------------------------------------
real*8, intent(in) :: cmap(:,:)
real*8, intent(in) :: t ! 0 <= t <= 1
real*8, intent(out) :: r, g, b
integer :: n, i
real*8 :: x, w
n = size(cmap, dim=1)
x = max(0.d0, min(1.d0, t)) * dble(n-1)
i = int(x) + 1
w = x - dble(i-1)
if (i >= n) then
r = cmap(n,1)
g = cmap(n,2)
b = cmap(n,3)
else
r = (1.d0-w)*cmap(i,1) + w*cmap(i+1,1)
g = (1.d0-w)*cmap(i,2) + w*cmap(i+1,2)
b = (1.d0-w)*cmap(i,3) + w*cmap(i+1,3)
end if
end subroutine cmap_rgb
!----------------------------------------------------------------
integer function bin_search2(xx, x, jlo0) result(jlo)
!----------------------------------------------------------------
! An accelerated bracket search that exploits locality to
! outperform binary search on correlated queries
!----------------------------------------------------------------
real*8, intent(in) :: xx(:), x
integer, intent(in) :: jlo0
integer :: n, inc, jhi, jm
logical :: ascnd
real*8 :: xlo, xhi
n = size(xx)
xlo = xx(1)
xhi = xx(n)
ascnd = (xhi >= xlo)
jlo = jlo0
if (jlo >= 1 .and. jlo < n) then
if (ascnd) then
if (x >= xx(jlo) .and. x < xx(jlo+1)) return
else
if (x <= xx(jlo) .and. x > xx(jlo+1)) return
end if
end if
if (jlo <= 0 .or. jlo > n) then
jlo = 0
jhi = n + 1
else
inc = 1
if (ascnd) then
if (x >= xx(jlo)) then
do
jhi = jlo + inc
if (jhi > n) then
jhi = n + 1
exit
end if
if (x >= xx(jhi)) then
jlo = jhi
inc = inc + inc
else
exit
end if
end do
else
jhi = jlo
do
jlo = jhi - inc
if (jlo < 1) then
jlo = 0
exit
end if
if (x < xx(jlo)) then
jhi = jlo
inc = inc + inc
else
exit
end if
end do
end if
else
if (x <= xx(jlo)) then
do
jhi = jlo + inc
if (jhi > n) then
jhi = n + 1
exit
end if
if (x <= xx(jhi)) then
jlo = jhi
inc = inc + inc
else
exit
end if
end do
else
jhi = jlo
do
jlo = jhi - inc
if (jlo < 1) then
jlo = 0
exit
end if
if (x > xx(jlo)) then
jhi = jlo
inc = inc + inc
else
exit
end if
end do
end if
end if
end if
do while (jhi - jlo > 1)
jm = (jhi + jlo) / 2
if (ascnd) then
if (x >= xx(jm)) then
jlo = jm
else
jhi = jm
end if
else
if (x <= xx(jm)) then
jlo = jm
else
jhi = jm
end if
end if
end do
! If outside range, clamp to last valid index
jlo = max(1, min(size(xx)-1, jlo))
end function bin_search2
!----------------------------------------------------------------
subroutine set_pl_margins(L,T,R,B)
!----------------------------------------------------------------
integer, intent(in) :: L,T,R, B
character(len=120) :: margintxt
character(len=*), parameter :: fmt1 = '(A,I4,A,I4,A,I4,A,I4,A)'
write(margintxt,fmt1) "%pl[margin=(",L,",",T,",",R,",",B,")]"
call winop@(margintxt)
end subroutine set_pl_margins
!----------------------------------------------------------------
integer function help_cb()
!----------------------------------------------------------------
integer :: iw
iw = winio@('%fn[Arial]%ts%bg&',1.2d0,rgb@(220,220,220))
iw = winio@('%ob%~bg[white]&')
iw = winio@('Colour map allows you to selection standard Rainbow/HSV colour map,%nl&')
iw = winio@('or the perceptually uniform colour maps Viridis or Magma, and also Turbo.%2nl&')
iw = winio@('Viridis, Magma and Turbo do not display phase angle in the pixel rendering.%2nl&')
iw = winio@('Increasing saturation increases color intensity (for rainbow/HSV only).%2nl&')
iw = winio@('Increasing minimum brightness raises the darkest pixels.%2nl&')
iw = winio@('Changing percentile changes the clipping of extreme amplitudes.%2nl&')
iw = winio@('Adjusting contour width changes the width of magnitude/phase rings.%2nl&')
iw = winio@('Contours can be blended towards a base white or black in Rainbow/HSV.%2nl&')
iw = winio@('Checking/unchecking contours toggles them on/off%2nl&')
iw = winio@('Checking/unchecking grid lines draws/erases the grid%nl%cb&')
iw = winio@('')
help_cb = 2
end function help_cb
end module domain_plot_mod
Below is a sample program which demonstrates the use of the code.
program test_domain_plot
use domain_plot_mod, only : domain_plot
implicit none
integer, parameter :: dp = kind(1.d0)
integer, parameter :: n = 300
integer :: i, j
real(dp) :: re_z(n), im_z(n)
complex(dp) :: f(n,n), z_temp, cj
cj = cmplx(0.d0,1.d0,kind=dp)
! Generate a test function
do i = 1, n
re_z(i) = -2.05d0 + 5.0d0 * dble(i-1) / dble(n-1)
do j = 1, n
im_z(j) = -2.0d0 + 5.0d0 * dble(j-1) / dble(n-1)
z_temp = cmplx(re_z(i),im_z(j),kind=dp)
f(i,j) = ((z_temp*z_temp - 1.d0)*(z_temp - 2.d0 - cj)**2 )/(z_temp*z_temp+2.d0+2.d0*cj)
end do
end do
! Plot function
call domain_plot(re_z,im_z,f)
! Generate second test functon
do i = 1, n
re_z(i) = -2.d0 + 4.d0*dble(i-1)/dble(n-1)
do j = 1, n
im_z(j) = -2.d0 + 4.d0*dble(j-1)/dble(n-1)
z_temp = cmplx(re_z(i),im_z(j),kind=dp)
f(i,j) = (z_temp-1.d0)/((z_temp**2)+z_temp+1.d0)
end do
end do
! Plot the second test function
call domain_plot(re_z,im_z,f)
end program test_domain_plot