Journal 'Nature' just published another paper where one of figures was made with FTN95 Clearwin native PL. This article reported how using advanced nanostructures to strip heavy atoms of most of their electrons utilizing relativistic laser pulses.
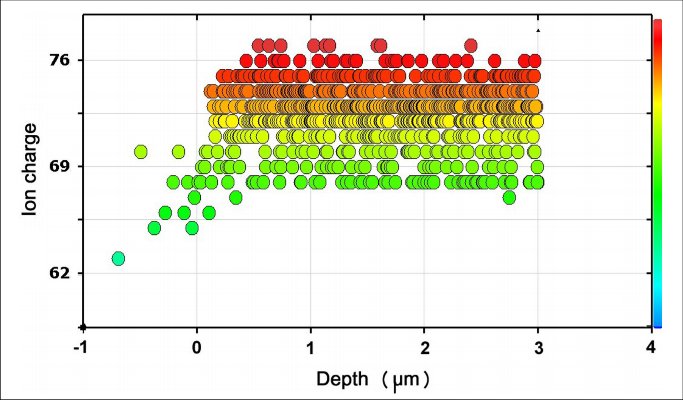
Native PL plot in the world top journal
Dan,
How do you get the x axis label of the %pl to include the greek letter mu i.e. your show micro metres with the correct SI symbol ?
One way is to call enable_utf8@(1). You can get the character by opening the Character Map dialog directly or from Plato. You don't need to set the font. The file must be saved using Advanced Save Options with 'UNICODE (UTF-8 without signature)'.
Thanks Paul, that works fine.
John, Example below:
module sine_mod
use clrwin
implicit none
integer, parameter :: dp = kind(1.d0)
integer, parameter :: n=360+1
real(kind=dp), parameter :: pi = 4.d0*atan(1.d0), deg2rad = pi/180.d0, sqrt2 = sqrt(2.d0)
real(kind=dp) x1(1:n), y1(1:n)
contains
integer function build_gui()
integer winio@, i
integer, save :: iw
x1 = (/(deg2rad*(i-1),i=1,n,1)/) ; y1 = sqrt2*sin(x1)
call enable_utf8@(1)
iw = winio@('%mn[Exit]&','exit')
iw = winio@('%fn[consolas]&')
call winop@('%pl[native, independent, x_array, n_graphs=1,gridlines,frame,y_min=-1.5,y_max=1.5, dy=0.5]')
call winop@('%pl[title='2π (rad) = 360°',x_axis=' Angle θ (rad)',y_axis=@]')
iw= winio@('%bf%ts&',2.d0)
iw = winio@('%pl&',600,400,n,x1,y1)
iw = winio@(' ')
build_gui =1
end function build_gui
end module sine_mod
program main
use sine_mod
implicit none
integer i
i = build_gui()
end program main
ALT + 0181
0181 have to be numeric pad digits
John
One way is to follow my directions above.
From Plato, goto to the View menu and select Character Map.
Find the character that you want and copy it to the clipboard.
Paste the character into your code.
Find the Advanced Save Options on the File menu, open the dialog and select UNICODE etc. as descibed above.
What is a 'relativistic laser pulse'?
Robert, It is when the laser field becomes so strong that it is capable to accelerate the electrons in one oscillation of the field close to their momentum M=mc and energy close to famous E=mc^2 = 511 keV (where m is electron rest mass and c is speed of light). At such intensities the relativistic effects start to dominate. In this work the laser was even 20x more powerful than that
